Método de resolución
Extremos
- Estudiar el dominio.
- Calcular la primera derivada.
- Puntos críticos: puntos candidatos a ser extremo. Aquellos que anulan la primera derivada junto con los extremos de los intervalos de definición si la función está definida a trozos.
- Calculamos la segunda derivada.
- Calculamos el signo de la segunda derivada en los puntos que anulan a la primera derivada:
- Si es negativa, es un máximo.
- Si es positiva, es un mínimo.
- Para saber si los extremos de los intervalos de definición son extremos, estudiamos la monotonía alrededor de dichos puntos.
- Estudiamos el signo de la derivada en los intervalos del dominio que generan los puntos críticos. Para ello escogemos cualquier punto de cada intervalo (el signo de la derivada no varía en los intervalos):
- Si es positiva: la función es creciente en el intervalo.
- Si es negativa: la función es decreciente en el intervalo.
- Los puntos de los intervalos de definición son:
- Mínimo: si la función decrece a su derecha y crece a su izquierda.
- Máximo: si la función crece a su derecha y decrece a su izquierda.
- No es extremo: si la función crece o decrece a ambos lados.
Ejercicios Resueltos
Ejercicio 1
SOLUCIÓN
Puesto que la función es polinómica, el dominio es todos los reales. Extremos: La derivada es |
Buscamos los puntos que anulan la derivada
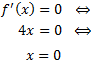
Estudiamos si los puntos críticos son extremos. La segunda derivada es
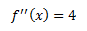
El signo de la segunda derivada en los puntos que anulan la primera derivada es
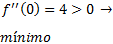
Puesto que se trata de una parábola, el mínimo, que corresponde al vértice, es un mínimo absoluto.
Monotonía:
Estudiamos el signo de la primera derivada en
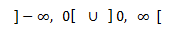 Escogemos cualquier punto de cada uno de los intervalos
Escogemos cualquier punto de cada uno de los intervalos
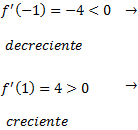 La función es decreciente en el primer intervalo y creciente en el segundo.
La función es decreciente en el primer intervalo y creciente en el segundo.
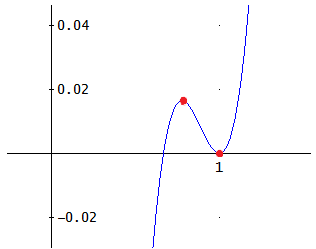
La gráfica de la función es
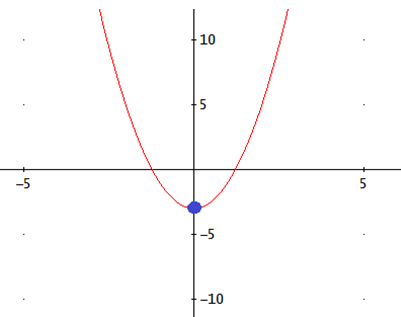
Monotonía:
Estudiamos el signo de la primera derivada en
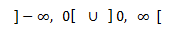
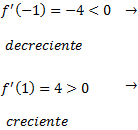
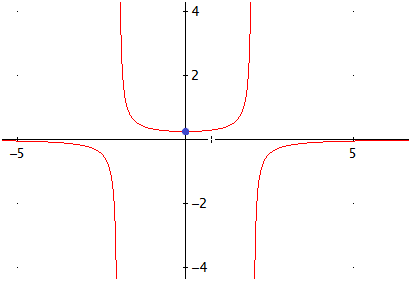
La gráfica de la función es

Ejercicio 2
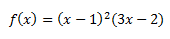 | |||
| |||
Ejercicio 3
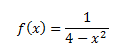 | |||
| |||


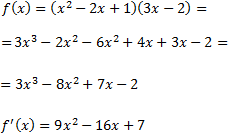
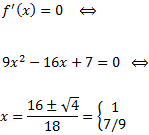
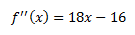
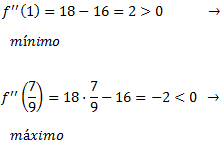
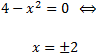
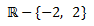
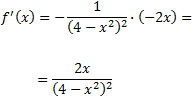
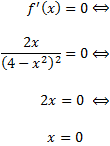
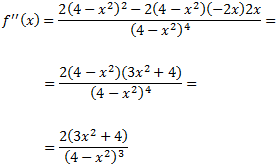
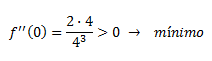
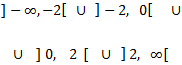
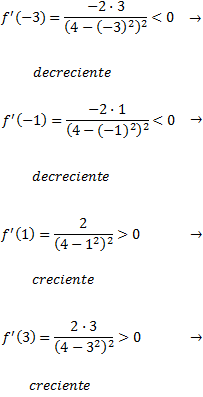








0 comentarios :
Publicar un comentario